TUBE OPERATION 3.
Fig 1. Schematic 30W PP class AB1 triode amp.
General operation with 6CG7, KT88 in triode.
Fig 2. Schematic Voltage Generator models of input stage and rest
of 30W amp.
Forward signal gain and backward GNFB gain calculations.
The paradox of GNFB which nobody understands, and how GNFB works.
Calculations of output resistance.
Fig 3. KT88 Voltage Generator model.
Fig 4. 6SN7 Voltage Generator model.
Fig 5. Schematic of 30W amp with 5 triode generator models and OPT
model.
Fig 6. Graph for open loop and closed loop gain F response with
12dB GNFB
without gain shelving and phase shift networks.
Fig 7. Graph for open loop and closed loop gain F response with
12dB and 16dB
GNFB with gain shelving and phase shift networks to compensate for
open loop phase shift.
Many associated issues explained and with recommendations for
Critical Damping, and use of Zobel R&C.
----------------------------------------------------------------------------------------------------------------
Fig 1.
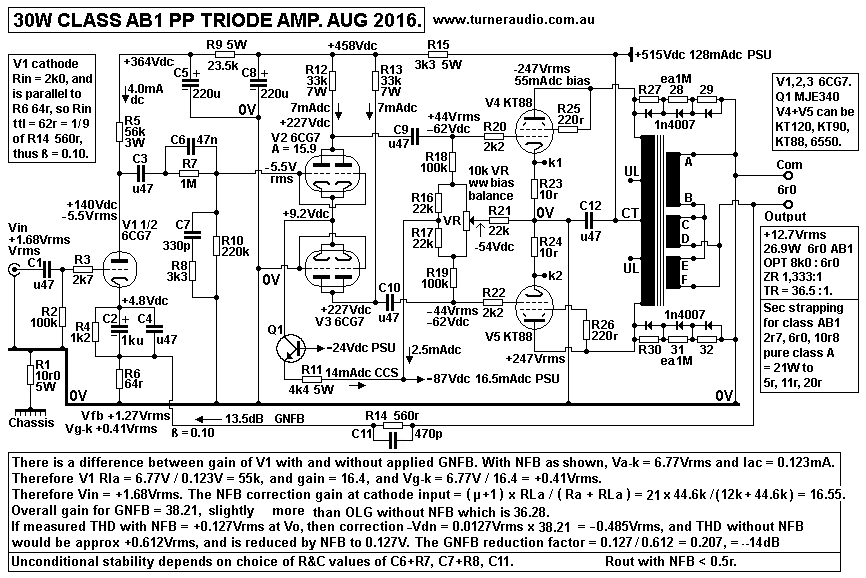
Fig 1 is a fairly simple 30W class AB amp is based on the 5050 UL
AB1
schematic at Integrated
5050.
The 30W triode amp has suitable schematic differences to 50W amp
to optimize performance with triode connected
KT88 or KT120, KT90, 6550. A quad of EL34 or KT66 could be used
with lower B+. But let me keep things simple
for awhile.
The basic operation :-
V1 = 1/2 6CG7, and is SET input triode in common cathode mode but
operating as a differential amp which produces a
single anode Va = Gain x difference between grid input and a
negative feedback signal from OPT secondary.
There are THREE figures for gain to consider. Without any GNFB,
ie, with R14 disconnected from R6, V1 gain
A = - µ x RLa / ( Ra + RLa ) = - 20 x 44.6k / ( 12k0 +
44.6k ) = - 15.76.
Vin = Vg-k =Va / A = - 5.5V / - 15.76 = +0.352V. The +/- signs
indicate relative phase. The gain without NFB is called
open loop gain because the NFB loop has not been closed with NFB
network R6 + R14. It is also "forward gain" because
it is produced by input producing signal increase from left at
input to right at output.
But with GNFB connected, the V1 Vgk increases to +0.41V because
the Vfb at V1 cathode = +1.27V, and there is increased
Va across V1 = 5.5 + 1.27 = 6.77V. The Iac remains the same as for
OLG and = 5.5 / 44k6 = 0.1233mAac.
Therefore we may conclude the effective V1 RLa = 6.77V / 0.1233mA
= 54k9, and tube gain is slightly increased to 16.41.
The Vgk = Va-k / A = 6.77V / 16.41 = 0.412V, quite a bit
more than what we calculated without any GNFB, so OLG with
NFB is actually LOWER with this type of single triode used as a
differential amp.
The other gain is BACKWARD where a fraction of Vo is fed back from
Vo to V1 cathode via R14 + R6 network.
The NFB applied to top of V6 has load of 64r and cathode input
resistance = RLa / A = 44k6 / 16.4 = 2k8.
This is parallel to R6 64r, so the NFB network really R14 560
feeding close to 62.2r so fraction fed back
ß = 62.2 / ( 560 + 62.2 ) = 0.10. This ß value is a common in tube
amps.
Any THD Vac applied to V1 cathode is amplified by V1 acting as a
grounded grid amp. The gain for grounded grid is higher
than for simple common cathode mode. For cathode input, gain =
( µ + 1 ) x RLa / ( Ra + RLa ) = 21 x 44.6k / ( 12k + 44.6k
)
= 16.55, and higher than the forward gain without GNFB of 15.75.
This is important to remember because calculations of
NFB reduction factor need to use the higher gain figure. More
about that below.
V2 plus V3 are each 6CG7 with both triodes in each in parallel so
that each of V2+3 make a triode with better capabilities
than if just one 1/2 6CG7 were used for V2 and V3. With 3.5mAdc in
each 1/2 6CG7, Ra = 13k, and for both triodes
Ra = 6k5 and the µ remains at 20 ( or close, depending on the
manufacturer ) The two 6CG7 tubes make two triodes
arranged as a differential amp, aka known as Long Tail Pair, LTP,
to make TWO balanced anode Va outputs with equal amplitude
but opposite phases. To achieve these outcomes, the R values of
RLa for each anode for V2+3 anodes must be closely
matched within 1%, easy in a world full of stable resistors with
1% tolerance.
Equal Va amplitude depends also on the commoned cathodes having a
constant current sink to a negative -Vdc rail.
Balanced input to both grids is not needed for output balance, ie,
Va amplitude equality. V2 grid is fed by V1 anode
output of -5.5V and V3 grid is to 0V, and for - 5.55Vrms at V2
grid you get 44Vrms at each anode, total gain
= 88V / 5.55 = 15.87.
Of course the very simple LTP, ( invented in about 1923 ) is not
quite that simple. V3 produces its output in grounded mode
because its grid is to 0V, and V2 cathode drives V3 cathode. Where
one grid is grounded, the gain of V2 is different to V3.
After doing an absurd amount of calculations I found that :-
Gain of V2+V3, ie, Va-a / Vg-g is no different to the normally
calculated forward gain = µ x RLa / ( Ra + RLa )
= 20 x 25.05k / ( 6.5k + 25.05k ) = 15.87.
You may find the common V2 Vgk is slightly more than V3 Vgk. If
there was balanced input to V2 + V3,
the gain of Va-a / Vg-g would remain constant, and common Vk would
be 0Vac. zero, except for some 2H, and that is
a story for another day.
V4 + V4 are KT88 strapped in triode mode, and set up for class
AB1, with fixed grid bias. They power a conventional
PP OPT with a nominal load ratio of 8k0 : 6r0. With idle Ea +500V
and Ia 55mAdc, idle Pda of each KT88 = 27.7W, so
they remain cool and happy to serve you over a long time. The
hotter tubes run, the shorter their life is, and sound DOES NOT
get any better with higher Pda than I recommend. The OPT with 8k0
: 6r0 will give 12W of initial class A, with maximum class
AB Po at 27W at clipping.
for maximum pure class A = Ea / Iadc - ( 2 x Ra ) for a single
power triode where Ra is the curve line for EG = 0V between
0.0mA and 2 x Iadc on the curve. This Ra curve is in effect the
triode "diode line" and for KT88 triode the resistance value
= 930r approx, so RLa for 500V x 55mA = ( 500V / 0.055A ) - ( 2 x
930r ) = 7,230r, say 7k2.
The theoretical max class A Po = 0.5 x Idc squared x RLa =
0.5 x 0.055 x 0.055 x 7,230 = 10.9W. In PP class A with 2 x KT88
triodes, each makes 10.9W for a total of 21W at secondary RL, and
the OPT must have a primary load = 14k4.
For only pure class A, RLa-a = 14k4, and the OPT sec RL should be
able to be a 4r0 speaker. I show the OPT with 8k0 : 6r0
strapping, but with provision for 8k0 : 2r67, 6r0, 10r7. If a 4r0
speaker is connected to 2.67r output, RLa-a = 12k0, and Po is
nearly all class A. If we wanted all class A the RLa-a must be
14k4, and we would need speaker Z = 4r7. But many speakers
of nominal "4r0" may have dips to 3r0, and much broader F ranges
of over 4r0, so the 2.67r outlet is looking good for any 4r0
speaker.
OPTs with 8k0 : 2r7, 6r0, 10r7 are just not mass made and must be
wound by an expert, and you will pay at least 3 times the price
of a mass produced item such as a 1650P from Hammond with 60W
rating for 6k6 : 4, 8, 16r.
Consider Hammond 1650P. If a 6r0 load is used with 4r0 output
terminals, the OPT functions with load ratio = 10k0 : 6r0,
and you will get 15W of pure class A with about 24W class AB which
should please just about everyone. The 60W rating for
6k6 means Va-a max = 629Vrms with Fsat at 30Hz, and with 24W into
10k0, Va-a = 489Vrms, with Fsat at 24Hz.
The Hammond quality resembles generic standards from 1960, and HF
response is minimal with the minimal amount of P & S
nterleaving, P-S-P-S-P, so making the amp unconditionally stable
for any value of pure C load will challenge DIYers who never fail
to completely mis-understand critical damping. There are a few
specialist makers of OPTs but ALL the ones I have ever known
will never disclose the specifications for turns,
core type, interleaving, winding resistance, leakage inductance,
etc, and you cannot ever calculate if what they wind will do the
job required by using the methods I have in my pages on OPT
design.
My experience tells me that KT88 with Ea 500V and Ia 55mA will
will give superlative class A Po in triode mode. For those
addicted to higher Po for slightly louder levels, Ultralinear taps
for screens can be used. I explain this in Integrated 5050.
For the 8k0 : 6r0 OPT with 6r0 load, and with Ea +500V, Ia 55mAdc
in each KT88 triode, where RLa-a is less than 14k4
for maximum possible Class A, Po is limited to what may be
calculated :-
Class A Po = 0.5 x RLa-a x Iadc squared, and for 8k0 we get 0.5 x
8,000r x 0.055A x 0.055A = 12.1W.
If you had RLa-a = 4k0, you would get 6W class A. The THD more
than doubles and damping factor halves for each time
you halve the RLa-a.
Using a 3r0 speaker with OPT 8k0 : 6r0 could cause tubes to
overheat at sustained high levels.
If you wanted to use a 1650P Hammond for only pure class A with
RLa = 6k6, then you would need to re-calculate the wanted
Ea and Ia :-
RLa-a = 6k6, so class A RLa per KT88 triode = 3k3.
With Pda = 30W at idle, expect 10W of class A Po.
Po = Iac squared x RLa, so Iac = square root ( Po / RLa ) = sq.rt
( 10 / 3,300 ) = 0.055mArms.
The minimum idle Idc = peak Iac = 0.055mArms x 1.414 = 78mAdc.
The Ea = Pda / Idc = 30 / 0.078 = +385V.
Check the RLa for max class A = ( 385V / 0.078A ) - ( 2 x 800r ) =
3,335r, so
RLa-a for 2 x KT88 = 6,671r, close enough to wanted 6k6. Total
Anode Po = 20W, and with 7% OPT losses in Rw
expect max class A Po at sec = 18.6W. You won't get much more
class AB Po with a lower RLa-a, so then you might
consider UL operation with 40% screen taps. This can double Po
with RLa-a = 3k6, but then the amount of GNFB must
be increased, the sonic outcome will be insignificant.
I first used a pair of KT88 in triode in a Quad-II amp in 1999,
see Fig 4a.
With fixed bias and Ea = +400V, Ia 60mAdc, I got 20W class AB for
RLa-a = 4k0 : 9r0, with first 7W in class A.
The owner treasures these amps. Best sound is where the speaker =
21r, and used on 9r0 outlet, giving RLa-a = 9k0,
somewhat impractical because nobody has 21r speakers.
The PSU for B+, heaters, and fixed -Vdc bias for KT88 grids and
CCS is similar to general principles used for integrated
5050 and YOU must decide whether you want to make a pair of
monoblocs or a stereo 3030, maybe OK to upgrade to
5050. This page is about tube operation, not power supplies.
The 30W amp schematic has some R&C networks which may seem
puzzling, but some are for stability and some to deliver
negative feedback to the V1 cathode.
The Least Understood aspect of amplifier function is Negative
Feedback followed by Phase Shift, Critical Damping, and Stability.
To have a better idea about NFB, the complexity of the tube amp
can be described with a more basic diagram :-
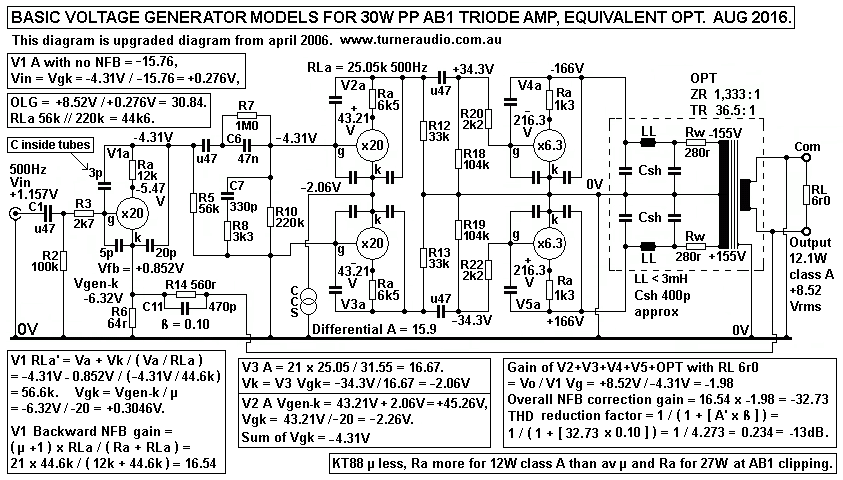
Fig 2.
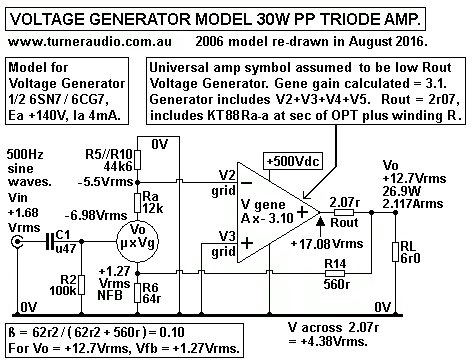
Fig 2 has two Voltage Generator models to describe the operation
of the 30W PP triode amp in Fig 1 above.
On left side is a model for V1 1/2 6CG7 which has Ea +140V, Ia
4mAdc, Ra 12k, and total RLa = 44.6k.
The cathode input resistance = Ra + RLa / µ = 56.6k / 20 = 2k8.
The NFB from output is applied to cathode via
R14 560r and R6 64r which is in parallel to 2k8, so the NFB
divider ratio = 560r : 62.5r, close enough to 9 : 1, which gives
ß,
the fraction of Vo fed back to V1 = 62.5r / ( 62.5r + 560r ) =
0.1004, close enough to 0.10.
On right side there is an equivalent Voltage Generator model for
V2+V3+V4+V5+OPT. Fig 1 shows the input to V2 grid
= -5.5Vrms which produces +12.7Vrms at OPT sec load = 6r0. The
gain with this load and the AB1 operation of
V4+V5 KT88 in triode = Vo / Vin = +12.7V / -5.5V = -2.309.
I have included the Ra-a and OPT winding resistance as an
additional Rout = 1r8 in series with RL 6r0.
The Ra-a of KT88 triodes varies from 1k3 to 900r from low Po in
class A to high Po in class AB. Therefore we can assume Ra
for calculations to be the average = 1k1 at clipping levels shown.
The two KT88 are effectively in series in a loop circuit including
Ra-a 2k2, total 7% winding Rw 560r, and total RLa-a 8k0. The sum
of Rw + Ra-a appears at sec = ( 560r + 2k2 ) / 1,333
= 2.07r, approximately.
Exact value of Ra can only be measured for a specific single value
of Ea and Ia. For this explanation of basic operation theory,
we may assume the average Ra. Measured Rout results should similar
to calculated or simulated results.
The whole operation of V2+V3 and KT88 act like a voltage generator
with effective - µ' = 3.22, and Rout' = 2r37.
(( We could say V2 grid has effective gm' = - µ' / Rout' = - 3.22
/ 2r37 -1.36A/V. The negative gm just means a negative going
Vac makes a positive going current. But with a voltage generator
model we need not consider gm )).
Without any GNFB and with 560r disconnected from Vo, approx -
5.5Vrms is still needed at V2 input to produce
Vo = +17.14Vrms at input side of Rout and +12.7Vrms at 6r0 load.
If the 6r0 load was removed, Vo would be +17.72Vrms
because Rout would have no Iac. Without the GNFB, the damping
factor with 6r0 load = RL / Rout = 6r0 / 2.37 = 2.53,
and if you had speakers with nearly constant Z, then the music
would sound fairly good at least up to about 15W, which
could be extremely loud if speaker sensitivity was 93dB/W/M.
With zero GNFB, the V1 triode has gain = µ x RLa / ( Ra + RLa
) = - 20 x 44.6 ( 12k + 44k6 )
= -15.75.
The presence of R6 64r causes some reduction of V1 gain by means
of local current FB.
V1 gain A' with 64r should really be A' = A / ( 1 + [ A x ß ] )
where ß = Rk / RLa = 64r / 44k6
= 0.00143, so A' = -15.75 / ( 1 + [ 15.75 x 0.00143 ] ) = -15.4.
Therefore Vin = Va / A' = -5.5V / -15.4 = +0.357Vrms.
Open loop gain with no NFB = Vo / Vin = 12.7V / 0.357 =
35.57.
Why are +/- signs used with Vac? - to indicate relative phase. V1
triode in common cathode mode is an inverting amp, so
that µ has a negative sign, and any + going input grid V will
produce a - going anode V. We can say the overall
Open Loop Gain, OLG, is the gain without NFB because the GNFB
network of R6 + R14 are not used to "close the loop".
I show the GNFB connected, and with the same Vo = +12.7Vrms to a
6r0 load. The V2 grid and V1 Va will still measure - 5.5Vrms.
The V1 cathode will have Vac = ß x Vo = 0.10 x 12.7Vrms =
-1.27Vrms. There is a total Va across V1 = - (1.27V + 5.5V ) =
- 6.77Vrms.
The apparent RLa powered by the V1 triode = Va / load current =
6.77 / 0.1233mA = 54.94k.
The V1 gain = - 20 x 54.9 / ( 12k + 54.9k ) = -16.41, and Vgk =
Vak / -A = -6.77 / - 16.41 = +0.4125Vrms.
There is anode flow in R6 64r in parallel with R14 560r
which gives Vac = R x Iac = 57r x 0.1233mA = + 007Vrms.
This would increase cathode Vac from 1.27Vrms to 1.277Vrms, a
change of +0.55%. Do we need to worry about such a tiny
consideration? I don't think so as long as the R6 value > V1
RLa / 500.
The V1 Vin = Vfb + Vcfb + Vg-k = 1.27V + 0.007V + 0.4125V =
+1.6895Vrms, say +1.69Vrms.
The Closed Loop gain, ie, CLG is gain with GNFB connected = Vo /
Vin = 12.7V / 1.69V = 7.517.
The connection of GNFB reduces gain by factor of CLG / OLG = 7.517
/ 35.57 = 0.2113.
The THD Vdn at Vo produces = ß x Vdn at V1 cathode. For Vdn, V1
acts in grounded grid mode where Gain for common grid
= +( u + 1 ) x RLa / ( Ra + RLa ) = 21 x 44.6k / ( 12k + 44.6k ) =
+16.54.
The gain from V2 grid to Vo = -2.309, same as for all signals at
V2 grid. Therefore backward NFB gain = 16.54 x -2.309 = -38.18.
Suppose we measure THD = + 0.1V at Vo with GNFB connected. This
would be 0.787% THD.
There is +0.01V THD at V1 cathode. This is amplified x -38.18 to
produce -0.382V at Vo.
But we cannot measure this at Vo, because we measure +0.1Vrms !!
So why do calculations produce a nonsense result with a larger
opposite phase THD Vdn to what we measure? The ONLY
conclusion we could make is that OLG +Vdn was a higher level that
what is measured with GNFB, and with GNFB, the amp
generates a -Vdn of opposite phase to reduce the high +Vdn without
any GNFB. In other words, THD +Vdn with
NFB = +Vdn without NFB - Vdn correction. Therefore +Vdn without
NFB = +Vdn with NFB + Vdn correction,
= +0.1Vrms + 0.382Vrms = 0.482Vrms = 3.8% THD.
THD reduction factor with GNFB = 0.1V / 0.482V = 0.207, or 1 /
4.82. Many Class AB1 tube amps can easily produce
3.8% THD without GNFB, and with GNFB the THD = 0.786%. The amount
of GNFB = 20 x log 0.207 = -14dB approximately.
To avoid so much applied logic with many small calculations, the
correct single GNFB formula for tube amps with SET input tube :-
THD reduction factor = 1 / ( 1 + [ A x ß ] ) where A is
backward gain for NFB and here it is 1 / ( 1 + [ 38.2 x 0.10 ] )
= 1 / 4.82 = 0.207 = -14dB.
The difference between forward gain and backward NFB gain is
seldom analyzed in text books which use just one figure for
gain being the forward gain without any NFB used to calculate THD
reduction factor. Using the OLG A without any GNFB,
THD reduction factor = 1 / ( 1 + [ 35.57 x 0.1 ] ) = 1 / 4.557 =
0.2195 = -13.5dB. In many cases the real world THD
reduction factor is not always what we calculate based on
perfectly conceived mathematics often because theoretical
Ra, µ, and gm are different to the real properties of tube samples
used. The calculations provide a guide, but having
+/- 2dB more or less NFB than we calculated will not make much
difference to the music or amp stability, and as long
as the R&C values are the same for 2 amp channels, then the Vo
of each channel with equal loads will be within +/- 0.5%
to give good stereo imaging.
All this reasoning and mathematics depends on the open loop phase
shift being less than +/- 5 degrees, and the OLG response
being flat. But all amplifiers are in fact active band-pass
filters. The open loop F response is only ever fairly flat, +/-
0.5dB for
between say 30Hz and 10kHz, and outside this range of F the
response falls and phase shift is result of a number of R&C
and L&R hi-pass and low-pass networks such as C + R couplings
from anode to next grid, and inductance in series with
output load or shunting output load.
The mathematics for gain and NFB would only predict behavior for F
in middle of AF band. I suggest use input Vac
between 400Hz and 1kHz. 500Hz is usually ideal. And you want Rout
of signal gene < 100r, and THD < 0.01%.
By use of X-Y axis on your oscilloscope, you may view the transfer
curve for Vo vs Vin. The two Vac levels may be
adjusted to produce a diagonal line from bottom left to top right
of CRO screen. Without NFB, the first part of line is
usually straight but then it curves over with less slope as the Vo
fails to be produced by the linear
Vo : Vin ratio as for low Po levels. If there is phase shift, the
transfer line will be become elliptical, and 90 degrees of
phase shift produces a circle. There are numerous online pictures
of CRO screens indicating phenomena in amplifiers.
There are a number of types of Feedback described in RDH4, 4th Ed,
1955. Some types are Negative FB, such as
series voltage ( used here in a power amp ), and shunt voltage (
used more in preamps ). Negative current FB also is
often used to lessen THD but increase Rout. Positive current FB is
used to lower Rout, but increases THD, and was
used sometimes in amplifiers in 1950s to fiddle with Rout to make
bass sound tighter. Rout could be made negative,
ie, the lower the load, the higher the Vo, and a short circuit
load would cause the amp to quickly oscillate to death.
Since about 1965, all amp makers abandoned any form of positive
FB, despite the mentions it gets in RDH4.
PFB makes too many reliability problems. But positive FB are an
indispensable tool to make an oscillator, which
is really an amplifier with a PFB loop. It may also have a NFB
loop to keep output level constant.
The Wien Bridge oscillator is a classic example.
The price we pay to reduce THD with NFB is a loss of gain.
Fortunately, it is very easy to get enough OLG in an
amp which is between 4 to 2,000 times the CLG with NFB. Many tube
amps have OLG = 200, but reduced to
20 so that 1Vrms input produces 20Vrms to give 50W into 8r0 load.
A solid state amp may also have same CLG,
but OLG = 20,000, and gain reduction factor = 0.001, and 5% THD is
reduced to 0.005%. They often sound worse
than the tube amp with 0.2% THD.
There is more to use of moderate amounts of NFB, say less than
20dB. Because of intermodulation effects, the
THD fed back will produce intermodulation harmonic products = sum
and difference of harmonic product from 2H
upwards and fundamental or lowest F, aka 1H. If 3H is the only
harmonic H, then NFB makes sum and difference
products with 1H, and so you see less 3H, but also some 2H and 4H,
where none existed without NFB. The badness
of such a phenomena is at its worst where THD = 10% and NFB is say
only 10dB. The 3H may be reduced -10dB,
but the 2H and 4H may be so high the sonic improvement with NFB is
almost negligible.
But the biggest problem with amplifier IMD is where you have
multiple IMD products produced between one or multiple
fundamental F and many IMD products are not harmoniously related
to the music; hence the amp makes a mess of
reproducing complex music signals which may include 50 singers and
a full orchestra. Speakers often make the same
mess especially where speaker drivers are forced to deal with more
than a decade of frequencies. Much research was
done between 1945 and 1975 on the 101 ways an amplifier can
degrade good music, and the issue of using GNFB or
not using it at all has propelled many heated arguments.
The THD is itself not the problem because all music has huge
numbers of harmonics related to the fundamental lowest note.
The THD describes the linearity, and the less linear an amp
becomes, the greater the the intermodulation H products.
If it was possible to remove the pure non distorted music from
what we hear at speakers, and just leave the IMD,
and possibly PSU noise, you may hear a quieter sound, but a
dreadful noise rising and falling with the level of the music.
We just need that level of background garbage to be as low as
possible. With tube amps, if THD < 0.1%, usually they
sound fine, and any extra effort to get THD down to 0.001% ( with
solid state ) may not make the slightest difference.
We need to remember :-
1. Try to arrange the tubes in the amp to produce THD < 4% THD
at -1dB below clipping without NFB.
2. Set up output tubes with idle Pda = about 2/3 of rating from
tube data.
3. PP amps to have nominal class AB load never less than 1/2 the
load for only pure class A.
This ensures a healthy and useful amount of initial class A is
likely to cover all listening needs except for high peak
level drumbeats or other transients.
4. Use at least 12dB GNFB with triode amps. For pentodes and beam
tetrodes, 20dB with pure pentode / tetrode,
15dB with 40% UL taps, 8dB with 20% CFB in output stage.
5. Never ask too much from your tubes. A pair of PP EL34 in triode
make a nice 12W.
Use sensitive speakers. Don't expect fidelity with a single EL84
in triode with a speaker 88dB/W/M and with loud levels.
But with headphones, the SE EL84 triode is unsurpassable!
6. Remember your ears produce a lot of harmonic garbage. Good
music has nothing to do with deafening levels heard
at a rock concert. At high levels, the amp and speakers may
continue to measure exceeding well, but your ears do not.
7. Best domestic stereo Hi-Fi listening is in a room which has
enough soft furnishings or carpets etc, to reduce
reverberations to a minimum. Don't blame the amp or speakers if
you have a terrible quality listening room.
There is no strict law about power. Just remember a pair of KT88
in Ultralinear or with CFB can give a nominal max
Po of 100W for 2 channels, and that's more than enough for all the
people I know, or have ever known, and 50W total is
usually plenty. If speakers have sensitivity 87dB/W/M, and your
average listening levels are 84 dB SPL, then total amp
power = 0.5W. For average SPL levels of 94dB, you need 5W, and for
104dB you need 50W.
Just remember your inconsiderate and uncouth neighbours may call
police if you insist on 94dB average levels with peaks
rising to 104dB. Speakers made in 1960 had featherweight voice
coils and cones to produce rated levels of up to about
95dB/W/M. So a pair of EL84 making 12W could make a high level,
but bass performance was usually very poor below 150Hz.
With many old "full range" and floor standing speakers the mid and
treble band levels may need -6dB attenuation above
100Hz to get a flat response from 50Hz upwards, so that the
sensitivity overall is much reduced because power is lost in
resistance attenuators. The issues regarding speaker impedance and
sensitivity is covered in my pages on Loudspeakers.
Output resistance of an amp should be fairly constant for any
power level. If it is not constant, then the gain will change
during each wave cycle and thus generate THD. Usually, SE tube
amps with only class A power have a fairly constant Rout.
But PP amps can have some Rout increase where Po is produced by
class AB above the initial class A region. Because
nearly all music is handled by the PP class A power, we only need
to know the Rout for this region of operation.
The Rout of a tube amp can be calculated if we know :-
1. Voltage gains of the input and driver stages,
2. µ of the output tubes,
3. Turn ratio of primary to secondary which is the unloaded
voltage ratio between
P and S windings,
4. Anode resistance, Ra of one output tube at the Q point.
Rout of the push-pull amp with FB applied = Rout = [ Ra-a
+ Rw total ] / [ ZR x ( 1 + { A" x µ x ß / TR } ) ]
Where Ra-a = twice the Ra of one output tube where two tubes are
used in a PP output stage.
TR is the P : S turn ratio for OPT, ie, unloaded P : S voltage
ratio at 1kHz,
TR also = square root of ZR, the P : load impedance ratio. Eg, OPT
for loads 8k0 : 6r0 has ZR = 1,333, and TR = 36.51 : 1.
Rw total is the sum of OPT primary winding wire resistance plus ZR
x secondary winding wire resistance.
A" = gain of input / driver stages preceding the output tubes, ie,
A" = Output tube Vg-g / Vg-k of the input tube.
The A" may be backward FB gain of V1 single triode x gain of
driver stage. µ is the amplification factor of an output tube.
ß is the fraction of OPT secondary voltage fed back to be "in
series" with the input voltage to V1.
For example in this case we have :-
Ra for one KT88 at 500V x 55mA = 1k3.
Ra-a = 2,600r.
Rw = 7% of primary RL of 8k = 560r ( including the sec Rw x ZR ).
TR = 36.5 : 1
ZR = 8,000 ohms : 6 ohms = 1,333 : 1,
A" = 15.0 x 16.1 = 241.5.
µ = 6.6 for KT88 at 500V x 55mA.
ß = 62.2 / ( 62.2 + 560 ) = 0.10.
Rout' = closed loop output resistance at the secondary output
terminals
Rout' for the above PP triode amp = [ 2,600 + 560 ] / [ 1,333 x (
1 + { 241.5 x 6.6 x 0.1 / 36.5 } ) ] = 0.441r
Model of the KT88 or 6550 triode as a Voltage Generator.
Let us better understand the output KT88 triodes in 30W amp in Fig
1 above.
Fig 3.
Imagine you have a magic box with unknown contents, but with 3
terminals. Imagine there is no Vdc or Idc between any
2 terminals, but there is a mystery circuit connecting all 3
terminals, and that the circuit will only respond to applied Vac
between say 50Hz to 10kHz.
Sooner or later, depending on your power to explore, measure,
analyze, and calculate, the box contents would look like
those in Fig 3, a low Rout generator where -1Vac applied across 2
terminals, say X and Y will produce +6.6Vrms across
Y and a third terminal Z, if measured with a high Zin voltmeter.
We might find that any other application of Vac just does not
give the same result. Then we find that we can connect Y to 0V,
and call it a cathode. We find Zin to X is over 1M0, so it is
like a grid, and that various loads connected from Z to Y
show that the there is an internal series resistance between Z to
Z
and = 1k3, and this looks just like a power triode anode.
We would conclude the mystery box behaves the same as a KT88
triode as I show in Fig 3, and with Ea = +500V,
Iadc = 55mA, Ra = 1k3, µ = 6.6, and gm = 5mA/V. You may find an
EH6550 in triode to be identical.
The 3 parameters of Ra, gm and µ can be measured in a test circuit
or an amp circuit but before building anything they can
be estimated from the triode data Ra curves for given values of
Eg1 bias. In this case above, idle Q point is at Ea = +500V,
Ia = 55mAdc.
Screens are connected to anode via 220r, and Eg2 = Ea = +500Vdc.
Ig2 may be about 5mAdc, included in the 55mA
quoted for Iadc, because the connection of g2 to anode makes these
two electrodes act as one electrode which is equivalent
to having a sheet metal anode placed where there existing g2
screen helical wire coil is now located. If a KT88 was to be
constructed without a screen g2, and to be equal to triode
operation, the anode might look like a smaller diameter metal tube
with wider fins to radiate the same amount of heat away. I once
asked a tube making company in Yugoslavia to build a
REAL TRIODE with µ about 7 and Ra about 1k0, with Pda max 50W, and
with indirectly heated cathode for 6.3Vac and an
octal socket. The company engineers's response was they already
had plans for this; but that was in 2003, and they were sitting
about drinking vodka. The able bodied workers were all still busy
rewiring the countries damaged wiring after the disastrous wars
in 1990s, and there was no money for fancy pancy vaccumy
thingamies. about. Nobody has bothered to build a really good REAL
TRIODE since about 1928 when Western Electric released the 300B
for movie sound - which nobody could buy - it was only
supplied in movie projector gear which was leased. But this old
triode is still being made, and has the same problem of the
directly
heated cathode, making the tube fragile and prone to microphony.
in 2016, The 300B from Emission Labs or KR Audio cost
more than 10 times a JJ 300B. But I digress.....
If a straight line is drawn on a KT88 triode data sheet through
Point Q and parallel to tangent through nearest Ra curve for Eg1
= -60Vdc, then the slope of the line has a resistance = Ea change
/ Ia change = Ra at the Q point, which I measured as 1k3.
The Ra at high Ea and low Ia will always be higher than the low Ra
quoted in data with lower Ea and higher Ia.
Looking along the horizontal Ia line for 55mA, we see that Eg1
change from -50V to -70V, Ea change is 428V to 560V, ie 132V.
Therefore µ = 132V / 20V = 6.6. The gm = µ / Ra = 6.6 / 1,300 =
5.08mA/V. These parameters are only valid for Ea and Ia
changes close to the Q point. But we may use them to get an idea
for the whole class A performance.
The generator output voltage can only be measured where RLa = CCS,
and then µ = Va / Vg. In this case, -31.1Vrms
would produce +205.4Vrms at anode, with a CCS. If load of 4k0 is
connected from anode to cathode, anode Va drops
to +155Vrms. The load Iac = 38.75mAac, and the V drop =
205.4V - 155V = 50.4V, so there is a resistance in series between
anode and generator = 50.4V / 38.75mA = 1,309r, say 1k3. Using
other loads of say 8k0, or 2k0 would all show there is series
R = 1k3. It is Ra, the dynamic anode resistance of the KT88 as a
power triode, a property due to the transconductance of the anode.
For KT88 beam tetrode operation with fixed Eg2, the same model
could be used where µ = 160, and Ra = 30k0 so that for
the same +155Vrms into 4k0 with 38.7mAac, there would be
+1,162Vrms across Ra 30k0, and +1,317Vrms at gene Vo and
Vg = Vgene / µ = 1,317 / 160 = -8.23Vrms, with gain = Va / Vg =
155V / 8.23 = 18.8. The gm quoted for KT88 data = 11mA/V,
but that is at Ia = 120mAdc, and at 55mAdc gm = 160 / 30k =
5.3mA/V.
The 1,317Vrms at V gene output is definitely never ever to be
measured even with RL = CCS. But if the Vg input were lowered to
0.5Vrms, and RLa = CCS, then we would see Va = µ x Vg = 160 x 0.5
= 80Vrms. For beam tetrode or pentode operation,
it is better to use the Current Generator Model explained in
Basic Tubes 1, see Fig 11.
This shows a 6AU6, but same method can be used for KT88 in beam
tetrode mode with different Ra, gm and µ.
Because tetrodes and pentodes have such a high µ, and Ra curves
are nearly horizontal, only the gm can more easily be read off
and estimated. The µ and Ra are both not easily estimated from
curves, but Ra is most reliably calculated by using 2 different
RLa,
say 4k0 and 8k0, using a fixed Vg = -1Vrms, and recording the Va
with each load.
Gain of each loaded condition = µ x RLa / ( Ra + RLa ), and
because RLa is known for each condition, and µ is the same for
both conditions, algebra can easily work out Ra, and then µ found
by substitution and gm = µ / Ra. In this case, where Ra =
30k, µ = 160, gm = 5.3mA/V.
The Current Generator model for tubes is better for beam tetrodes
or pentodes. Grandfather's generation knew all these useful
tricks to understand how tubes work, but hardly anyone I know now
knows anything.
Here is another model for a single 1/2 of a 6SN7, 6CG7, or 6J5...
Fig 4.
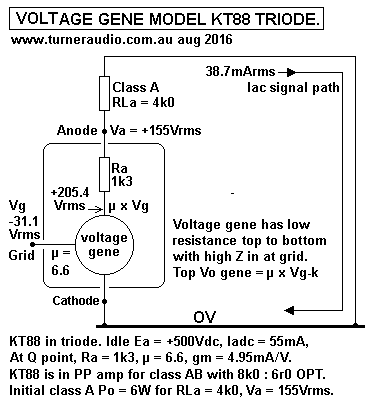
Fig 4 is for 1/2 6SN7 but could be 1/2 6CG7 for V1 in 30W triode
amp in above Fig 1. Ra = 12k, µ = 20, RLa = 44k6. Gain = 15.76.
The V2 and V3 in 30W amp are each both halves of 6CG7 with Ia =
3.5mAdc each for total of 7mAdc. Ea = +218V,
and the Ra of each 1/2 = 13k, so paralleled triodes have Ra = 6k5,
while µ remains 20, and gm = 3.08mA/V.
Their total RLa = 25.05k, and gain = -20 x 25.05k / ( 6.5k +
25.05k ) = -15.88. ( negative because gain inverts Vgk )
Here is the whole Fig 1 triode amplifier modeled more fully......
( Even grandpa had trouble figuring it all out ! )
Fig 5.
Anyone can see this isn't any easier to understand than the actual
amp schematic in Fig 1 at top of this page.
Most R & C numbers correspond to numbers used in Fig 1.
Each triode is drawn as a Voltage Generator with a series Ra
resistance. There are capacitors shown between anode,
cathode, grid of all 5 triodes, which consist of static C values
within each tube and includes whatever stray wiring C
exists to act in the same way.
These C values are not fully known but could be determined by
those keen enough. The effect of such C, all under 100pF
is to cause phase shift and loss of gain at F > 50kHz.
The C between grid and anode of all tubes causes increased input C
at all grids = gain x C and this is the Miller effect.
The gain shelving and phase shift reduction networks of C6+R7,
C7+R8, and R14+C11 are shown but may need to be
quite different if your OPT has different properties. However, the
effect of these networks is negligible for 500Hz.
There is enough information to allow a Bode Plot of open loop F
response to be drawn after another 50 calculations or
by simulation program.
The OPT is drawn with a classic equivalent RLC schematic and L and
C values are very approximate because no two
brands of OPTs are the same, These shunt C and leakage inductances
cause a loss of gain and increasing phase shift
above 10kHz, and also load output tubes with series or parallel
resonant networks above 20kHz.
We initially want to know all gain / FB effects at a mid
frequency, and worry later about the fact the amp is an active
bandpass filter with a global loop of NFB. Ideally, the response
without GNFB will have -3dB points F1 and F2 between
20Hz and 20kHz, and the GNFB should widen the response from 7Hz to
65kHz, at 1/2 full rated Po with the nominal RL.
Peaks in sine wave response near F1 and F2 should be less than
+1dB. Without any R load, and at 1/4 full Vo level, any
value of C between 47n and 4u7 should not cause HF oscillations or
square wave ringing exceeding +6dB, and not settling
within 30uS.
Sine wave response peaks with pure C loading should not exceed
+6dB at any F to 1MHz, not cause more than +1dB
increase in all F levels < 20kHz. The use of the rated RL
parallel with any value of C should much reduce response
peaking and square wave ringing with a 5kHz square wave.
Before we could ever properly test an amp for gain and GNFB THD
reduction at 500Hz, the amp may well oscillate
without the R&C networks shown, so the values I give may be
initially used, but will later need to be optimized.
The open loop gain is of most importance with beam tetrode or
pentode output tubes because their Ra is many times the
Ra for triode so that a KT88 or 6550 in beam tetrode may have µ =
180, Ra = 30k, gm = 6mA/V at 500V & 55mA.
The gain with RLa = 4k0 = 21, and without any RL the gain = µ =
180, about 28 times the triode gain with no RL.
Without any GNFB, the increase of GNFB with no RL = +3dB approx,
but with pentode the GNFB increase would
be from 21 to 180 which increases GNFB by +19dB, a huge increase,
and very likely to cause LF and HF
oscillations with no R load at output. Ultralinear amps or those
with CFB are slightly prone to the same problem
depending on the UL tap % or CFB%.
Usually, the R7 + C6 prevent LF oscillations in nearly all amps.
The R8 + C7 plus C11 may not give full stability at HF
with a C load = 0.47uF. I do not show a typical Zobel across
output sec terminals of say 5r6 + 0.33uF. Sometimes this
causes square wave ringing to get worse, and perhaps Zobel network
of 3k9 + 1nF may be connected across each 1/2
primary of OPT.
The overall mission plan should be to maximize the F response with
a pure R load at FULL PO and without any tube
in the amp saturating or driven into grid current, while
ensuring the amp will not oscillate under any circumstances
whatever.
Sadly, very many old brand-name amps and some not so old could
oscillate badly and all too easily.
The easiest way to determine Rout with NFB connected is set up the
amp with rated RL and set Vo = 1/2 the clipping level.
Measure and record this Vac. Calculate Iac = Vac / RL. Without
change to input Vac, remove the RL, and measure and
record Vo, which should have increased slightly. This the Vo
without any Iac.
Calculate Rout = ( Vo No RL - Vo with RL ) / Iac with RL . For
example, say Vo = 6Vrms to 6r0. Then Iac = 1A.
Without 6r0 RL, Vo = 6.5Vrms. Rout = ( 6.5V - 6.0V ) / 1.0A =
0.5r.
The tube line up shown in Fig 1 and 3 will provide very adequate
open loop bandwidth compared to amplifiers using
pentode input tubes such as EF86 or 12AX7 inputs, or use of
similar for differential driver amps as in Mullard 520.
The 520 and others were often built by many enthusiasts in the
1950s and 1960s but DIYers used very poor OPT with
high LL and Cshunt and with low primary inductance so that some
samples could not be turned on without a load
connected and they would not drive electrostatic speakers. While
Mullard may have liked us all to use high Ra pentodes
and triodes for the driver tubes I would always prefer the low Ra
low µ triodes for signal stages which are less affected
by stray C effects and Miller capacitance. The Williamson amp with
6SN7 input and driver tubes had open loop bandwidth
> 200kHz, far better than anything Mullard recommended.
Use of a 0.22uF at Vo without RL make a C reactance load = 7.2r at
100kHz. It is often enough to cause an extra
90degrees of phase shift to add to what is already there so if
gain > 1.0 at 100kHz and phase shift > 180d, the amp will
oscillate at HF.
The test load for ESL speakers is usually a 1r5 in series with 2uF
with say 15r across all. All amps should cope well
with such a load at 1/2 full Po. The total load value is about 4r5
at 20kHz, with load change from 15r at LF to about 1r8
at 200kHz.
There is no easy way to set up any tube amp with GNFB and make it
unconditionally stable unless you understand how
to reduce ringing on square waves with say 0.47 across Vo with no
RL, and using 5kHz square waves. I have often used a
10k pot + radio tuning cap to find best R&C values for R8
& C7 and R11. R11 must not be too large or else too much
very
high F will get to V1 cathode to cause HF oscillations. Zobel
network R across OPT primary or sec should have high Watt
rating lest they cook while testing at HF.
Here are some typical graphs which the audio enthusiast can plot
using a sine wave generator and CRO :-
Fig 6.
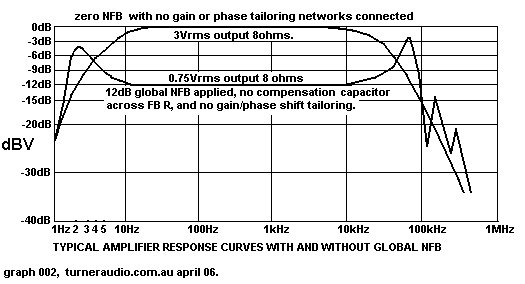
Fig 6 graph shows the sine wave response in a very ordinary tube
amp with average quality OPT without NFB and with
NFB, and with no attempt to tailor the open loop gain or phase
shift to prevent the peaks in sine wave response just outside
the audio band. The responses here are with the amp loaded with a
resistance only. The LF peaks are due to LF phase
shift so that between 1Hz and 5Hz there is perhaps more than
110degrees of phase lead so that the FB which is applied
is so much out of phase with the input signal that little gain
reduction occurs due to the 12dN of applied FB. At HF the
situation is similar at 60kHz, and the dips and peaks above 100kHz
are due to output transformer resonances series or
parallel L&C combinations of leakage inductance stray shunt
capacitance between windings.
To be able to measure a tube amp with global FB isn't always easy
with a high amount of NFB applied initially.
A basic circuit without any correction RC networks will often
oscillate quite badly as soon as any NFB is connected
for the first time. For any new amp, the FB used should be 6dB
then 12dB, and if it doesn't oscillate, one is very lucky,
but usually the response for sine waves is peaked as in the above
graph, and steps must then be taken to decide on
values of the RC compensation networks and zobel networks. When
all that is done properly, a graph of the amp with
networks in place will more likely resemble the graphs in Fig
7.....
Fig 7.

Notice that the open loop gain has been reduced at the extreme
ends of the audio band and the rate of phase shift
increase for frequencies where oscillation may possibly otherwise
occur has been reduced. With a very good OPT,
it is possible to apply up to about 40dB of global NFB into a pure
resistance load. A good OPT would give you an
amp with 3Hz to 65kHz of bandwidth without any NFB connected at
least and with few resonances above 80kHz.
The bandwidth of the tubes and their couplings must be wider than
the OPT to be able to measure the open loop
bandwidth of the OPT. Whether tubes output tubes are triodes or UL
or beam tetrodes all has some effect on
outcome but all can be tamed by critical damping networks
mentioned.
Many OPT are not capable of being used with more than 16dB GNFB. I
have only ever used a maximum of 35dB
of GNFB with very good OPTs before it became impossible to make
the amp stable. This meant the margin for
stability was virtually 0.0dB and any addition of say 0.1uF across
Vo would cause oscillations, and removal of RL
would also cause oscillations, all in the presence of maximal
Zobel gain tailoring. But the same amp had its GNFB
reduced to 12dB and the margin of stability was then 22dB, a vast
improvement. I've worked on many amps near a
disaster with only 3dB margin of stability.
For another graph and notes and schematic details for dealing with
problematical amplifiers go my web page on
'Leak Amplifier re-engineering'
, where considerable phase tweaking is used to obtain healthy
bandwidth into a R
load and unconditional stability for a 1954 Leak TL12 Point1 which
has an awful OPT. I have used all the tricks
available to tame the Leak. There is a Zobel network across the
output to 0V. I tried Zobel networks from V1
anode to 0V, and across the OPT primaries, but they did little to
reduce response peaking or improve the square
wave response so I relied on the negative current FB operating
above 20kHz and the normal shunting of the global
NFB resistance with a small cap. The Leak thus gives healthy
bandwidth with some peaking in the response but it
ended up much more stable than in the original circuit.
Zobel values should be about as follows :-
V1 anode to 0V, R = 1/10 of total ac and dc RL in parallel, C
should have its reactance in ohms = 1/10 V1 RL
at 100kHz. Use a pot and a radio tuning gang to establish correct
values if this Zobel is used; wrong values will
worsen the outcome and cause more peaking and less bandwidth for R
loads, thus reducing the margin of stability.
Eg, where RL = 30k, R = 3.3k, C = 470pF.
Zobel across each half of OPT primary. R = Class A RLa-a /
2, C has reactance = R at 100kHz. Eg, RLa-a = 8k,
so R across each 1/2 P winding from B+ to each anode = 3.9k, and
wire wound, with C = 390pF min to maybe 1,000pF.
Zobel across the whole output secondary of OPT.
Consider the 30W amp in Fig 1 which would have at least 4 primary
sections interleaved with 3 Secondary sections :-
1. Secondary with sub-sections for multiple winding strapping, 2
sections each 2N turns, 1 section with 2 x 1N turns.
This allows output turns to be 2N for 2r67, 3N for 6r0, and 4N for
10r67.
If we insist on having Zobel R&C, three are needed, 2r7+1uF
for 2r67, 5r6+0.47uF for 6r0, and 10r0+0.27uF for 10r67.
Not one manufacturer has ever provided this. It is all too much
expense and confuses each and every audiophile when they
try to change strappings to change load matching every 3 months to
get a better sound with different speakers.
Therefore, it is probably better to not try to use Zobel R&C
across multiple output secs and only use Zobel R&C across
1/2 primary windings.
BUT where there are multiple secondary windings set for ONLY ONE
output load, then a Zobel R&C is forgivable,
and ensures the amp load has become close to the nominal R at
100kHz which will be found to help prevent oscillations
above 75kHz.
2. Tapped Secondary with 3 identical windings of 4N turns, all
paralleled for 10r67, 3N 75% tap = 6r0, 2N 50% tap = 2r67.
Only one Zobel R&C with 12r0 + 0.18uF is needed across the
whole 4N turns.
I don't show Zobel R&C across output of Fig 1 30W amp because
the OPT has multiple secondary windings which can be
strapped in 3 different ways to get 3 different load matches for
8k0 : 2.67r, 6r0, 10.67r.
This website has numerous schematics of complete power amps where
I used Zobel R&C in various ways to ensure there
was no possibility of any HF oscillation.
If in doubt, set up a work bench with good lights and plenty of
tools, and build, measure and analyze, and never stop
asking questions, to avoid remaining ignorant.
Forward to
Basic Tube 4
Back to
Basic Tube 2
Back to Index Page




